LFE Friday - digraph:get_path/3

This week's LFE Friday was translated with permission from the Erlang Thursday series by Steven Proctor. This week's translator: Robert Virding.

Today's LFE Friday is on digraph:get_path/3.

digraph:get_path/3 takes a graph, a starting vertex, and an ending vertex and will attempt to find some path through the graph of length greater than zero, where all vertices in the path are distinct, except allowing for the first and last vertices to be the same.

If a path is found, it returns a list of the vertices visited (in order) to complete the path, if no path is found, false is returned.

First we will setup a new graph that we can traverse.

> (set graph (digraph:new))
#(digraph 8207 12304 16401 true)
> (set v-1 (digraph:add_vertex graph 'v-1))
v-1
> (set v-2 (digraph:add_vertex graph 'v-2))
v-2
> (set v-3 (digraph:add_vertex graph 'v-3))
v-3
> (set v-4 (digraph:add_vertex graph 'v-4))
v-4
> (set e-1 (digraph:add_edge graph v-1 v-2))
($e . 0)
> (set e-2 (digraph:add_edge graph v-2 v-3))
($e . 1)
> (set e-3 (digraph:add_edge graph v-3 v-4))
($e . 2)
> (set e-4 (digraph:add_edge graph v-2 v-4))
($e . 3)
> (set e-5 (digraph:add_edge graph v-4 v-1))
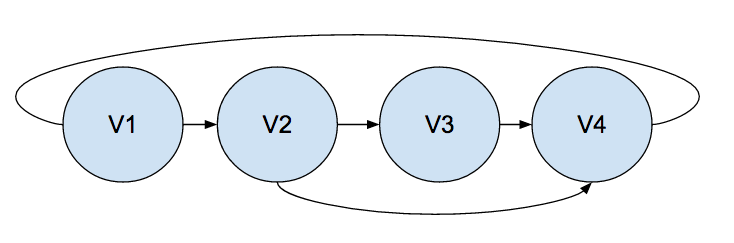
($e . 4)

We label the vertices to make it easier to see the paths. This will give us a graph that looks like the following:

Now we can get to playing with digraph:get_path/3 and see what the paths are from any sets of nodes.

> (digraph:get_path graph v-2 v-3)
(v-2 v-3)
> (digraph:get_path graph v-2 v-4)
(v-2 v-4)
> (digraph:get_path graph v-2 v-1)
(v-2 v-4 v-1)
> (digraph:get_path graph v-3 v-1)
(v-3 v-4 v-1)
> (digraph:get_path graph v-1 v-4)
(v-1 v-2 v-4)
> (digraph:get_path graph v-1 v-1)
(v-1 v-2 v-4 v-1)

Note that these just happen to be the shortest paths, but this is not guaranteed to return the shortest path, but just the first path found.

And if we add a new vertex, and don't connect it to any other node in the graph, and we call digraph:get_path/3, we can see it returns false.

> (set v-5 (digraph:add_vertex graph 'v-5))
v-5
> (digraph:get_path graph v-1 v-5)
false

- Proctor, Robert